Führen Temperaturschwankungen zu Längenveränderungen von Rohren, sorgen Ausgleichsbefestigungen und Fixpunkte dafür, dass sich Rohre in beide Richtungen ausdehnen können.

Mit zunehmendem Temperaturanstieg der durchströmenden Flüssigkeit …
Rohrleitungen wie Heizungs- oder Warmwasserleitungen, die sich während des Betriebes einer haustechnischen Anlage erwärmen und wieder abkühlen, dehnen sich je nach Werkstoff unterschiedlich aus. Kälteleitungen dagegen können um eine bestimmte Länge schrumpfen.
Beispiel: Eine sieben Meter lange PE-Rohrleitung dehnt sich bei einem Temperaturanstieg der durchströmenden Flüssigkeit von 20 auf 60 Grad Celsius um 56 Millimeter aus.

… dehnt sich das Rohr aus.
Wie groß die jeweilige Längenänderung sein kann, bestimmen
Es empfiehlt sich bei Berechnung der Längenveränderung, die Temperaturdifferenz nicht nur normaler Betriebstemperaturen, sondern maximal möglicher – wie etwa bei einem Störfall – zu berücksichtigen. Auch spielt die Einbautemperatur eine Rolle. Wird zum Beispiel an einem heißen Sommertag im Deckenbereich einer Lagerhalle eine Leitung installiert, können dort hohe Temperaturen auftreten.
► Die am höchsten zu erwartende Temperaturdifferenz berücksichtigen.
Zur Berechnung der Rohrlängenänderungen dient die Formel:
∆L = L × α × ∆T [mm]
∆L = max. Längenänderung des Rohres [mm]
L = Länge der Rohrleitung [m]
α = Ausdehnungskoeffizient [mm/(m × K)] (s. „Ausdehnungskoeffizient“)
∆T = max. Temperaturunterschied [K]
Rohrmaterial: Stahl
Rohrlänge: 20 Meter
Tmin = +55° C
Tmax = +70° C
Einbautemperatur (TEinbau): +20° C
∆T = Tmax − TEinbau
∆T = 70° C − 20° C
∆T = 50K
∆L = L × α × ∆T [mm]
∆L = 20 m × 0,012 mm / m × K × 50K
∆L = 12,0 mm
Mögliche Längenausdehnung des Rohres: 12 Millimeter
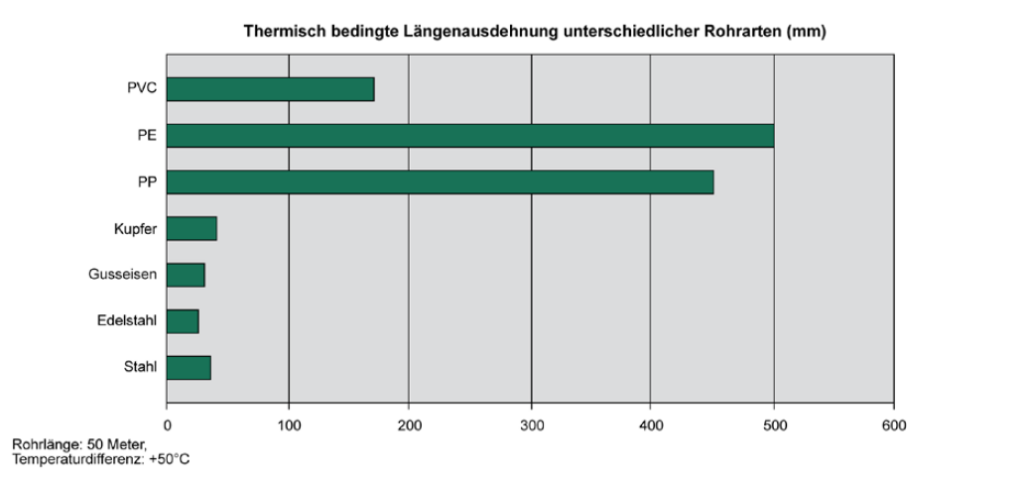
Rohrmaterial: Edelstahl
Rohrlänge: 50 Meter
Tmin = +6° C
Tmax = +12° C
Einbautemperatur (TEinbau): +35 ° C
∆T = TEinbau − Tmin
∆T = 35° C − 6° C
∆T = 29 K
∆L = L × α × ∆T [mm] ∆L = L × α × ∆T [mm]
∆L = 50 m × 0,010 mm / m × K × 29 K
∆L = 14,5 mm
Mögliche Schrumpfung des Rohres: 14,5 Millimeter
Der thermische Längenausdehnungskoeffizient α gibt die Längenänderung eines einen Meter langen Körpers bei einer Temperaturänderung von einem Kelvin an:
α = mm / (m × K) = Längenausdehnung in Millimetern / (verlegte Rohrlänge in Metern × Temperaturänderung in Kelvin)
Die Längenausdehnung in Millimetern (mm) ergibt sich abhängig von der verlegten Länge in Metern (m) und der Temperaturdifferenz in Kelvin (K). Je länger das verlegte Rohr und je höher die Temperaturdifferenz, desto stärker die gesamte Ausdehnung. Da Längenausdehnungskoeffizienten experimentell bestimmt werden, können die Werte in verschiedenen Tabellen unterschiedlich sein. Für besondere Rohrtypen ist der Koeffizient beim jeweiligen Rohrhersteller einzuholen.
Thermischer Längenausdehnungskoeffizient α ausgewählter Materialien
| Rohrmaterial | mm/(m × K) |
|---|---|
| Stahl | 0,0120 |
| Edelstahl | 0,0100 |
| Gusseisen | 0,0115 |
| Kupfer | 0,0170 |
| Kunststoff - PB | 0,150 |
| Kunststoff - PE | 0,200 |
Eingeplante Dehnungsmöglichkeiten kompensieren auftretende Spannungen und verhindern Schäden in der Rohrleitungsanlage und am Bauwerk.
Längenveränderungen können ausgeglichen werden durch:
In Rohrsystemen mit häufigen Richtungswechseln (z. B. L- oder Z-Bögen) ist die Längenausdehnung der einzelnen Teilstrecken meist so gering, dass sie über die Befestigung (Gewindestangen, Schallschutzeinlage der Rohrschelle) aufgefangen werden kann.
Ist ein häufiger Richtungswechsel nicht gegeben, können unter Einsatz von U- bzw. Lyra-Bögen Dehnungsschenkel erzeugt werden. Reicht das dafür vorzusehende Platzangebot nicht aus, müssen Kompensatoren in die Rohrleitung eingebaut werden. Diese nehmen Bewegungen des Rohres auf und gleichen sie aus. Bei der Planung und Montage von Kompensatoren ist auch der Anlageninnendruck von Bedeutung.
Um Flexibilität zu garantieren, bleibt ein so genannter Biegeschenkel frei. Wie groß er sein muss, hängt ab
Berechnung der Biegeschenkel-Mindestlänge Lb:
Lb = K x √da x ΔL
Lb = Länge des Biegeschenkels [mm]
K = Materialkonstante (da materialabhängig, vom Rohrhersteller einzuholen)
da = Außendurchmesser des Rohres [mm] ∆L = max. Längenänderung des Rohres [m]
Siederohr nahtlos nach DIN EN 10220 DN65 (76,1 x 2,9 mm) mit einer maximalen Betriebstemperatur von 70 °C, einer Einbautemperatur von 20 °C und einer Leitungslänge von 40 m (20 m Teilstrecke).
K = 90
α = 0,012
∆T = 50 K
L = 20 m
da = 76,1 mm
∆L = L × α × ∆T (s. „Erwartete Längenänderung – Berechnung“)
∆L = 20 m x 0,012 mm / m x K x 50 K
∆L = 12 mm
Lb = K x √da x ΔL
Lb = 90 x √76,1 mm x 12 mm
Lb = 90 x √913,2 mm2
Lb = 90 x 30,22 mm
Lb = 2719,8 mm
Länge des notwendigen Biegeschenkels: 2 719,8 mm
Fixpunkte werden bei Rohrleitungen mit großer Ausdehnung eingesetzt. Sie führen die Ausdehnung in Richtung eines Kompensators oder eines Dehnungsbogens, um auftretenden Kräften entgegenzuwirken. An einem neutralen Punkt installiert, bieten sie Rohrleitungen in beiden Richtungen vom Fixpunkt aus Spielraum. Zwischen den Fixpunkten montierte Gleitstücke ermöglichen dem Rohr freie Ausdehnung. Diese Gleitpunkte (Gleitrohrschellen oder -führungen) bilden schiebende Halterungen zwischen Festpunkten. Dabei ist zu beachten, dass ein Gleitwiderstand auftritt und die dadurch entstehenden Kräfte auch vom Fixpunkt aufgenommen werden müssen.
Bei einem Dehnungsbogen ist die Distanz der ersten Führungsschelle bis zum Bogen äußerst wichtig. Je kleiner die Distanz, desto größer sind die benötigten Kräfte, um den Bogen zu biegen und die Rohrausdehnung aufzunehmen. Die dabei entstehenden Kräfte werden auf den Fixpunkt übertragen.
Zur Auswahl des richtigen Fixpunktes ist es notwendig die folgenden Parameter zu kennen:


Whitepaper zum Fachbeitrag anfordern
Technisches Merkblatt „Längenausdehnung bei Rohren“ herunterladen